Na proizvoljno orijentiranoj, cjelovito strukturiranoj površini svakog kristala pa tako i snježnog mogu se naći sljedeći strukturni oblici. Prvo, tu su facete (ravne, glatke površine paralelne jednoj od kristalnih ravnina koje sadrže visoku površinsku gustoću atoma). Nadalje tu je i najvažniji objekt, stepenica, postojanje kojeg omogućuje rast kristala. 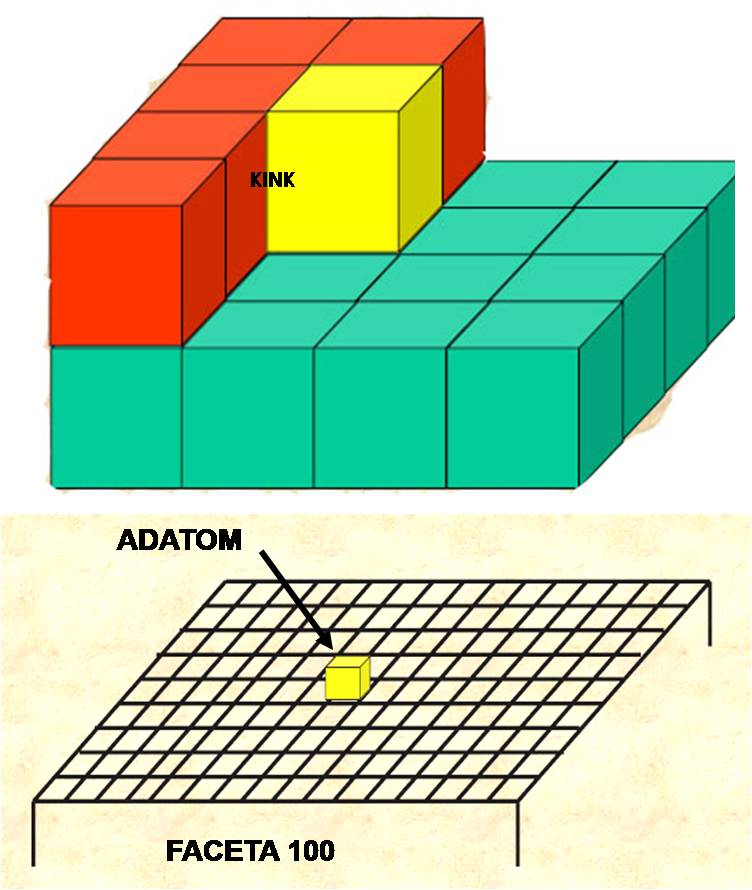Stepenica čini rub facete ili prijelaz iz jedne paralelne ravnine (terase) u drugu jednoatomnim visinskim razmakom. Na kraju imamo i kinkove. To su jednoatomni lomovi na stepenici na koje nailazimo krećući se duž stepenice. Stepenicama su inače premrežene sve zakrivljene plohe, površina između susjednih stepenica naziva se terasa.

Na mikroskopskoj razini postoji 5 različitih kristalografskih mjesta na površini kristala, koja su dostupna molekulama iz pare [4,5,6]. Razlikuju se po energijama potrebnim da se molekula s određenog mjesta odvoji od površine kristala i prebaci u paru. Lako je uočiti da molekule na tim mjestima ostvaruju različit broj kemijskih veza s molekulama u kristalu koji čine njihovo najbliže susjedstvo. 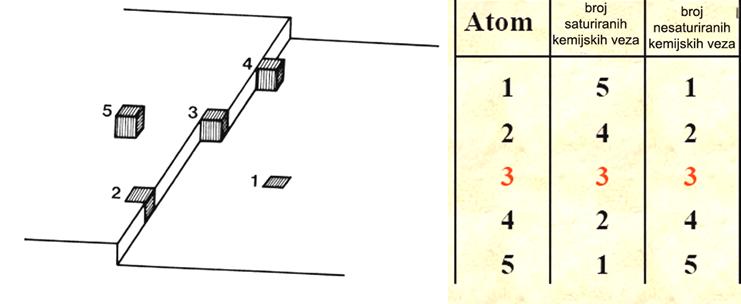Energija mjesta proporcionalna je sumi produkata broja prvih, drugih, ..., susjeda i jakosti odgovarajuće (za pojedine susjede) kemijske veze.

Na Slici 12., za slučaj jednostavne kubične rešetke, prikazana su sva kristalografski i energijski relevantna mjesta. Najslabije je vezan atom u položaju 5 (inače adatom na faceti ili terasi daleko od stepenice, vidi Sliku 13.b). Ograničimo li se samo na prve kristalografske susjede adatom (5) ostvaruje samo jednu vezu i to s atomom u kristalu ispod njega, što znači da mu preostaje 5 nerealiziranih veza. Dakle, rezultat dovođenja atoma na položaj 5 jest jedna saturirana veza, jedna prenesena nesaturirana veza i 4 novostvorene nesaturirane veze. Predstavimo li atom kockom onda je sjedanjem atoma na položaj 5 stvorena nova površina koju čine 4 bočne plohe kocke (preostale dvije od 6 su: jedna je prenesna od podnožja na tjeme kocke, a jedna je nestala). Atom na broju 5 ne oslobađa saturiranjem jedne veze dovoljno energije da stvori tako veliku novu površinu (4/6 'površine' atoma), pa je taj proces malo vjerojatan. To ne znači da nije u svakom trenutku moguće 'vidjeti' mnoge pojedinačne atome na facetama i terasama koji tu provedu jako kratko vrijeme da bi se ponovo vratili u paru. Pri malim brzinama rasta njihov utjecaj je zanemariv jer zbog termičke nestabilnosti nisu objekti koji omogućuju nastavak rasta. Na površini provode vrlo kratko vrijeme i ne ugrađuju se u nju. No nisu bez uloge u jednom drugom modusu rasta, dvodimenzionalnoj nukleaciji.

Potpuno suprotna situacija je s položajem broj 1 u kojem je atom najjače vezan za kristal, dakle ima najnižu energiju (5 kemijski saturiranih veza i jedna nesaturirana). Iako energijski povoljan, popunjavanje tog položaja pri rastu ima također malo utjecaja na brzinu rasta jer broj takvih mjesta u normalnim okolnostima iznimno malen.

Atom na položaju broj 4, inače adatom stepenice, iako češći kao uspješni događaj pri rastu nego adatom facete (broj 5), također je manje važan u globalnom rastu kristala. Njegova energija niža je od energije 'broja 5' (jače je vezan: 2 realizirane i 4 nezasićene veze, od toga 2 nove nezasićene veze). Komplement mu je atom u položaju broj 2 (rupa u stepenici ili vakancija) s 4 zasićene i 2 nezasićene veze.I taj položaj zbog malog broja nije ključan pri rastu kristala.

Najznačajniji za kontinuirani rast kristala je pložaj broj 3 ili KINK položaj. U tom položaju atom ima tri zasićene i tri nezasićene veze. Najvažnije jest da atom koji se ugradi u kink položaj ne mijenja broj nezasićenih veza, pa tako ni površinu kristala. Za efikasnost rasta važno je da se ugradnjom atoma u kink položaj broj kinkova ne mijenja. Naime, efikasnost rasta ekvivalenta je energiji potrebnoj da se ugradnjom atoma izgradi nova površina. Podsjetimo se da kod položaja s brojem 5 to nova površina iznosi 4/6 'površine' atoma (stranice kocke), kod 4 to je 2/6, kod kinka (3) to je 0/6, to jest nema povećanja. Ostala dva mjesta karakterizira smanjenje površine, odnosno kod 2 to je -2/6, i kod 1 to je -4/6.

Dakle, u dobroj aproksimciji, možemo reći da se proces rasta odvija preko kinkova koji ne mijenjaju veličinu površine pa tako ni površinsku energiju. Površinska energija mijenja se na većoj skali. Prvo, pri formiranju jednoatomne stepenice te, u nastavku, pri svakom povećanju duljine stepenice sve dok novostvoreni sloj u cijelosti ne pokrije stari sloj.

Sadržaj
Uvodna riječ
Oblici pahuljica
Snježna pahuljica – što je to?
Fazni dijagram vode
Povijesni pregled
Kristalna struktura
Zašto se istražuju pahuljice
Rast u laboratoriju
Dijagram oblika pahuljica
Rast pod mikroskopom
Kontrola rasta građom površine
Površinsko taljenje leda
Kontrola rasta difuzijom
Dendritski rast
Literatura

<< >>