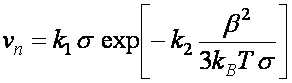a) o mikroskopskoj strukturi površine kristalića leda i

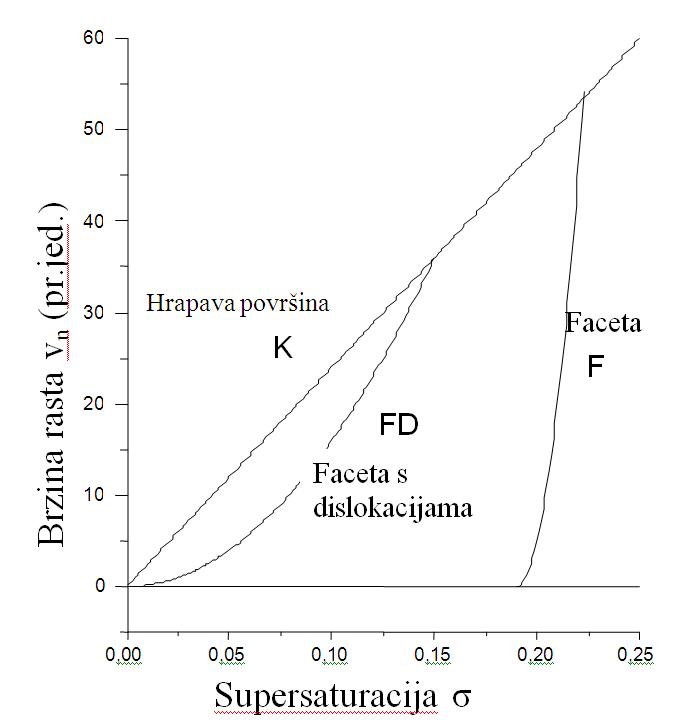
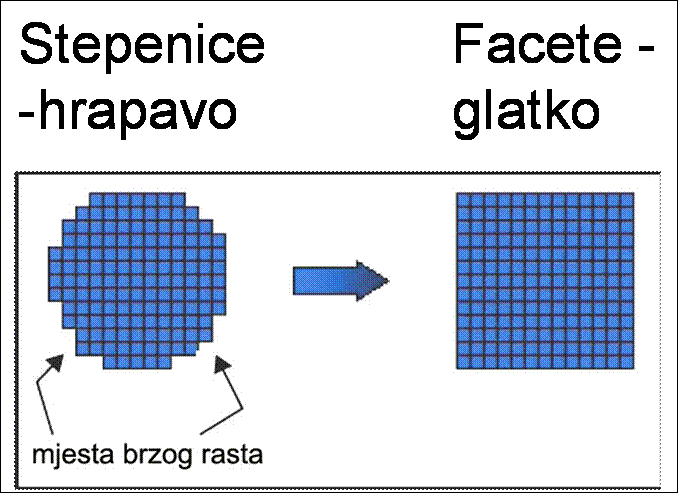
b) o brzini difuzije molekula vodene pare kroz zrak na putu od pothlađenih kapljica vode iz najbližeg susjedstva do površine kristala.

Raspravimo prvo kako izgled površine na atomskoj/molekulskoj razini utječe na brzinu rasta i na konačne oblike kristala

Razmatranje rasta kristala na mikroskopskoj razini sugerira da kristal, da bi monotono rastao, mora imati jako velik broj kink - položaja kako bi u svakom trenutku mogao primiti svaki pristigli atom ili molekulu. Naravno to vrijedi za umjereno jake struje dolazećih molekula na površinu kristala iz okoline. Smještanjem molekula u kink položaje broj kinkova se ne mijenja. Kinkovi su 'nered' na ravnim uredenim stepenicama, a posljedica su termički aktivacijskih procesa. Iako im je broj jako ovisan o temperaturi s povišenjem temperature brzo saturiraju (dosegnu maksimalnu gustoću). Dovoljno daleko, niže od temeprature taljenja broj kinkova je saturiran i maksimalan, pa tako praktički neovisan o daljnjem porastu temperature. Opisanu površinu kristala sa stepenicama i kinkovima zovemo hrapavom.

Ako je pak površina glatka, a to znači bez stepenica i kinkova, kristal može rasti samo kad se ispune određeni uvjeti. Takvu površinu zovemo facetom. Da bismo potaknuli rast potpuno facetiranog kristala nužno je na faceti formirati stepenicu (zapravo otočić od jednog sloja atoma rub kojega čini stepenicu), na kojem se, zbog relativno visoke temeperature i dinamike, spontano formiraju kinkovi. Kinkovi pa čak i jača meandriranja stepenica fluktuacije su oblika, karakteristične i svojstvene kristalima. Proces stvaranja otočića naziva se dvodimenzionalna (2D) nukleacija, a rast se smatra aktivacijskim. To je inače pojava koja se kod rasta kristala još uvijek istražuje, fizikalni principi koje nisu do kraja poznati.  

U opisanim uvjetima rast će se odvijati samo ako postoji dovoljno jaka sila koja gura molekule iz jedne faze u drugu. Ta sila (izvedenica supersaturacije) u osnovi je ovisna o nadtlaku ili nadkoncentraciji u odnosu na ravnotežne veličine. Brzina rasta kristala u nekom smjeru definira se kao prirast linearne dimenzije voluminoznog kristala u jedinici vremena. Može se mijenjati od točke do točke na površini, a za naše potrebe uzima se kao brzina rasta komponente radijus vektora normalne na površinu kristala i označava kao v_n. Ona je linearno proprcionalna supersaturaciji (σ) ako je površina hrapava.

Ako je pak površina glatka rast se neće odvijati (ili će biti krajnje spor) sve dok supersaturacija ne dosegne kritičnu vrijednost dovoljnu za formiranje stabilne stepenice (otočića), da bi zatim rast, zbog obilja kinkova na rubu otočića, fizikalno postao skoro kao da se radi o hrapavoj površini. To traje dok sloj ne izraste u cijelosti. Nakon tog potreban je opet novi otok. Treba reći da stvaranju stabilnog otočića prethodi veliki broj neuspjelih pokušaja u kojima se otočići začmu, ali se rasprše prije nego zažive. Proces pokušaja i raspadanja je stalan i odraz je fluktuacija termodinamičkog sustava kristal - okolina.

Kao da se radi o preskakanju barijere pa se proces smatra aktivacijskim. Rast ovisi o sposobnosti stvaranja inicijalnih otočića na glatkoj faceti. Brzina rasta, u tom slučaju, formalno je opisana sljedećim izrazom  

gdje β predstavlja energiju za formiranje stepenice jedinične duljine, T je apsolutna temperatura, a k₁ i k₂ su geometrijske i dimenzijske konstante, dok je k_B Bolzmanova konstanta. Za male supersaturacije σ eksponent je znantno veći od 1 pa je vjerojatnost formiranja stepenice, nužne za rast, zanemarivo mala. Kad σ postane dovoljno velika da se eksponent približi vrijednostima za koje se eksponencijalna funkcija počinje razlikovati od nule, počinje i detektibilan rast Takav rast zovemo nukleacijski rast jer širenju svakog sloja po površini facetiranog kristala prethodi nukleiranje stabilnog dvodimenzionalnog otoka nadkritične veličine. Rast facete izrazito je nelinearan. U pravilu, brzina rasta faceta bitno je manja nego za hrapavu površinu (vidi Sliku 14.) osim kad je σ tako velika da rast prijeđe u kaotični. U tim uvjetima proces rasta naziva se kinetičko hrapavljenje jer je površina zatrpana strujom nadolezećih atoma ili molekula tako da se ne stigne relaksirati ni u jedan od stabilnijih oblika. Nadolazeći atomi samo 'vide' obilje raspoloživih kinkova i tu se s lakoćom smještaju.

Na Slici 15 prikazan je proces rasta u dva vremenski udaljena trenutka. Rast počinje s kuglastim, a završi s potpuno facetiranim kristalićem. Ovo je čest uzorak za proces prijelaza hrapave površine u glatku. Glatke površine ili facete pojavljuju se kod mnogih kristala pri rastu zato što neke površine rastu znatno brže nego druge. Pri kontinuiranom rastu kristali su to facetiraniji što im je supersaturacija manja. Prijelaz s hrapavog prema facetiranom obliku se susreće i kod rasta snježnih pahuljica, poglavito kod niskih supersaturacija, i to bez obzira na temperaturu. Naime hrapava površina, ako nema nekih usporednih procesa ili specifičnosti, raste brzo i smanjuje svoj udio u ukupnoj površini. S druge strane supersaturacija je premala da nukleira nove otočiće odnosno nove stepenice za rast pa kristal poprima potpuno facetirani oblik i time dramatično smanji brzinu rasta. Narasli oblici su prizme, a omjer dimenzije bazične i bočne plohe poprima različite i prilično neobjašnjive vrijednosti (vidi Sliku 11). Jednako neobjašnjivom pokazuje se ovisnost brzine rasta o temperaturi.

Inače, opisani uzorak prelaska s hrapavog oblika na facetrirani prati svaki modalitet rasta. Procesi i mehanizmi o kojima će biti govora i koji će biti raspravljeni svaki u svojoj podlozi ima opisani prijelaz.

Sadržaj
Uvodna riječ
Oblici pahuljica
Snježna pahuljica – što je to?
Fazni dijagram vode
Povijesni pregled
Kristalna struktura
Zašto se istražuju pahuljice
Rast u laboratoriju
Dijagram oblika pahuljica
Rast pod mikroskopom
Kontrola rasta građom površine
Površinsko taljenje leda
Kontrola rasta difuzijom
Dendritski rast
Literatura

<< >>