 |
||
|
Kontola rasta difuzijom molekula vode kroz zrak (ili kako objasniti rast šupljih stupića, konveksnih
(ispupčenih) površina, pojavu grananja, dendrite,...) Pogledajmo sada
drugi važan čimbenik koji u najvećem broju slučajeva odlučuje o obliku snježnih
pahuljica. On se odnosi na parovitu fazu i način na koje molekule dolaze na
površinu kristala. Snježni kristalić pri rastu opskrbljuje se molekulama iz svoje najbliže okoline u kojoj
se nasumce gibaju molekule vode. Slikovito govoreći, čim se jedna molekula
ugradi u površinu nju difuzijom iz okoline nadomještaa druga. Treba se prisjetiti
da su izvor molekula vode fina suspenzija pothlađenih vodenih kapljice u zraku.
One su spremnik koji podržava određenu koncentraciju vodene pare odnosno njen
parcijalni ravnotežni tlak,. Svaku molekulu koja se ugradi u kristal nadomješta
molekula koja je isparena s, recimo, obližnje sićušne kapljice vode. Isparenoj
molekuli treba izvjesno vrijeme da se probije u blizinu rastućeg kristala. Na
svom putu sudara se molekulama zraka kojih u pravilu ima znatno više.). Proces
putovanja sa sudaranjem naziva se difuzijom. Brzina kojom se nadomještaju za
rast potrošene molekule određena je koeficijentom difuzije. Koeficijent
difuzije ovisi o tlaku gotovo uvijek prisutnog zraka jer vjerojatnost sudara s
molekulama zraka proporcionalna koncentraciji molekula zraka odnosno (ekvivalentno)
tlaku zraka. Ako je brzina rasta kristala ili potrošnje bliskih molekula vode
velika, a brzina dotoka molekula iz dalje okoline mala, kontrolu rasta preuzima
proces dotoka odnosno difuzija molekula u zraku. Koeficijent difuzije
ovisi o temperaturi. Pri analizi
slučaja kada je difuzija kontrolor brzine rasta, kristal smatramo i tretiramo kao
spremnik uređenih molekula. Kristal unosi promjene u raspodjelu koncentracije molekula
oko kristala jer tik uz površinu ima svojstvenu koncentraciju molekula vode i
ekvivalentni ravntežni tlak para. U uvjetima visoke, dobre difuzije uvijek ima
dovoljno molekula uz površinu kistala, koje dolaze s kapljica i koje
koncentraciju drže nepromjenjivom i jednakom ravnotežnoj koncentraciji vodenih
kapljica. Ukupna promjena koncentracije vodene pare s one karakteristične za
kapljicu do one karakteristične za kristala zbije se praktički na dimenziji usporedivoj
s debljinom površinskog sloja kristala. U uvjetima slabe difuzije promjena
koncentracije raširi se na udaljenost znatno veću od dimenzije snježnog
kristala. Da bi prikaz bio što zorniji, a objašnjenje što jednostavnije preskočit ćemo
strogi formalni postupak opisivanja događanja [1]. Koncentracija vodene pare u zraku,
u sustavu kristala, ima dvije fiksne točke: minimalnu, na površini kristala,
karakterističnu za kristal, s jedne strane, i maksimalnu, vrlo daleko od
kristala, (kažemo u beskonačnosti), karakterističnu za pothlađenu vodu (vidi
Sliku 03), s druge strane. Ako kristal aproksimiramo materijalnom točkom
ili pak, materijalnoma dužinom rješenje difuzne jednadžbe daje raspodjelu
koncentracija u prostoru oko kristala. Ono je sferno simetrično odnosno
elipsoidno koncentracijsko polje. Koncentracija se radijalno i
kontinuirano mijenja od minimalne do maksimalne (proizvoljno daleko od
kristala). Na Slici 16 prikazane su izokoncentracijske (ili
izosupersaturacijske) linije. Kristal, međutim, ima konačnu dimenziju i realni
oblik (facetirana heksagonska prizma). Oblik unosi određene promjene u elipsiodno
polje koncentracije molekula.
|
Sadržaj |
|
|
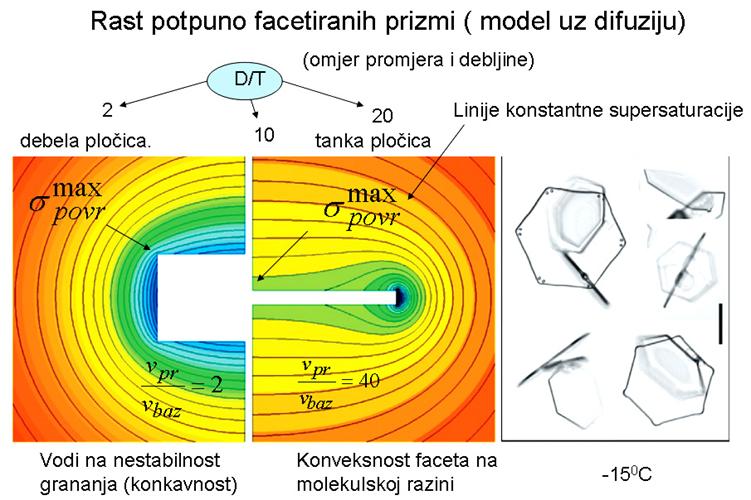
Slika 16: Supersaturacijsko polje u blizini površine kristala oblika prizme [1] |
||
|
Na Slici 16 prikazana su dva polja koncentracije, tlaka para ili supersaturacije vodene pare za slučaj najjednostavnijeg prizmatskog oblika kristala za dva tipična oblika heksagonske pločice i heksagonske prizme. Koncentracijsko polje predstavljeno je linijama konstantne koncentracije odnosno supersaturacije (supersaturacija je maksimalna u crvenom polju na rubovima slike, a minimalna uz površinu kristala u plavom dijelu polja). Lijevo polje poremećeno je (perturbirano) debelom, tzv. izometrijskim prizmom (prikazan je presjek ravninom paralelnom heksagonskom osi) kojoj je dijametar bazne plohe 2 puta veći od debljine kristala (bočne plohe), a desno tankom pločicom (jednaki presjek) kojoj je navedeni omjer 20. Pretpostavimo, ono što se čini očiglednim pri rastu prizmi malih dimenzija (sve dok prizme izgledaju kao prizme), da su vertikalne brzine rasta ploha konstantne duž pojedine plohe. Zatim, radi očuvanja oblika prizme, treba specificirati omjere brzina rasta bočne i bazne ravnine. Brzine rasta su uostalom eksperimentalno mjerljive. Na lijevoj slici treba pretpostaviti omjer 2, a za desnu on je 40. Rješenje jednadžbi (Laplaceove i jednadžbe kontinuiteta) za pretpostavljene rubne uvjete pokazuje da površinska supersaturacija (ona koja potiče rast) varira znatno duž površine facete. U predstavljenoj dvodimenzionalnoj slici (cilindrična aproksimacija 3D problema) supersaturacija za lijevo polje najviša je na bridovima i brzo pada prema sredinama i baznih i bočnih ploha. Posljedica je da rub raste brže nego li sredina plohe i ploha poprima konkavni oblik (udubljena ploha vidi Slika 17, ref. [11] )
Slika 17: Prizma s konkavnim plohama; pojednostavljena simulacija; rast kontroliran difuzijom [10] Za desno polje supersaturacija je najveća na sredini bočne plohe pa je rezultat rasta konveksna ploha bazna tj pločica izgleda kao atletski disk (bacačka sprava). Opisana analiza ponudila je kvalitativni okvir za razumijevanje pojavnih oblika mnogih snježnih pahuljica koje rastu u uvjetima umjerene supersaturacije; i onih diskastog napuhnutog oblika (sektoriranje je daljnja komplikacija porijeklo koje leži u anizotropiji površinskih svojstava) kao i onih šupljih prizmi i stupića (Slika 18). Granica koja dijeli konkavne od koveksnih prizmi jesu heksagonalne pločice kod kojih je promjer bazne plohe 10 puta veći od visine (bočne plohe).
|
||
|
piše dr. sc. Zlatko Vučić Institut za fiziku, Zagreb |
||

 Slika 18:
primjerci šupljih stupića [1]
Slika 18:
primjerci šupljih stupića [1]