Postoji i više od navedenog kad je riječ o rastu kristala - prizmi u uvjetima kontrole rasta difuzijom molekula vode kroz zrak. Sve dok ploha uspijeva ostati ravna aktualan je scenarij po kojem se konkavnost koncentrira na samoj sredini plohe. No, znamo da vidljivo izobličenje ravne glatke plohe, pa ni konkavnost, nije moguća bez stepenica. Ono što je očito je sljedeće: na bridovima, zbog pojačane supersturacije (lijeva Slika 16) događa se pojačani rast brida, u usporedbi s ostatkom kristala, a rezultat su iza sebe ostavljene stepenice (ili nedovršeni rast sloja za slojem) koje se šire prema sredini plohe kontinuiranim popunjavanjem (donji dio Slike 19).

Promjena jakosti supersaturacije po plohi sugerira da je gustoća stepenica najveća u sredini plohe. Po uvjetima rasta centar plohe predstavlja hrapavu plohu. Kako smo vidjeli na Slici 14, za danu (umjerenu) supersaturaciju hrapava ploha raste najbrže. Stoga, sredina plohe jedno vrijeme lako rastom sustiže rubove i održava makroskopski privid ravne plohe. Kako se veličina plohe povećava, povećava se i hrapavost. Kad hrapavost dosegne maksimum sredina plohe ne može više pratiti rubove i polako zaostaje, pa ploha kao cjelina sve više pokazuje konkavnost. (vidi gornji dio Slike 19).

Jednostavne heksagonske prizme rastu u uvjetima normalne difuzije molekula vode. Normalni uvjeti su sljedeći: difuzija umjerena ili visoka, veličina kristala mala, supersaturacija niska i tlak zraka rekltivno nizak. Poremete li se značajno vrijednosti navedenih veličina (tlak zraka poraste ili supersaturacija poraste ili kristal značajno naraste) to je istovjetno značajnom smanjenju koeficijenta difuzije.

Tada počinju dolaziti jače do izražaja učinci mehanizma difuzije. Naime, pri rastu kristal 'hvata' molekule iz zraka, ali iz bliske okoline koje pak trebaju biti nadomješetene onima iz udaljenijih mjesta. To priječi brži rast kristala, ali otkriva proces koji je poznat pod nazivom Mullins-Sekerka nestabilnost. Navedeni koncept prilično dobro objašnjava zašto narasle pahuljice pokazuju tako raznolike i razgranate oblike.

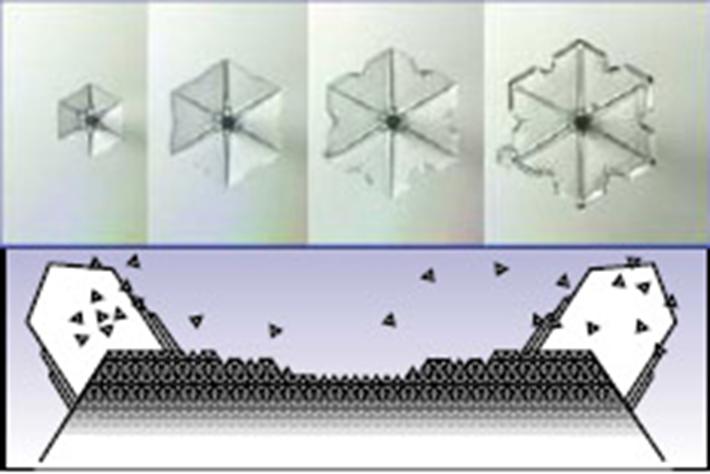
Kako je već spomenuto, bridovi heksagonske prizme strše više od ravnih dijelova kristala pa im je lokalna supersaturacija veća. Zbog toga je molekulama koje difundiraju lakše doći do bridova nego do sredine ploha. Zato bridovi rastu brže. Bridovi, kao u 2D prikazu na Slici 16, postaju klice koje sežu sve dalje u parovitu fazu i time nailaze na sve veću supersaturaciju (Slika 20). Nastaje je pozitivna povratna veza koja potencira bujanje klice u duljinu. Točnije naš heksagonski kristal pokazuje 6 prilično jednakih tankih grančica jer su uvjeti rasta prilično jednaki za sve izdanke na dimenzijama kristala od oko mm (čak i ako nisu jednaki, zbog dinamike zraka, vrlo je vjerojatna rotacija kristala što ujednačuje eventualnu nesimetriju krakova-klica). Vrlo brzo, tijekom rasta klica, i bočne strane svake od 6 klica/grančica dođu u uvjete Mullins-Sekerka nestabilnosti i rađaju svoje vlastite izdanke – grančice, uvijek čuvajući heksagonsku simetriju. Na kraju opetovano grananje može dovesti do čudesno razgranatih oblika koje i ne tako rijetko susrećemo u prirodi.

Prilično jednostavan spoj spore difuzije molekula i pozitivne povratne veze tijekom rasta izdanaka (bridova koji razdvajaju bočne plohe) heksagonske prizme leži u temelju kompleksnosti, pojma koja najbolje opisuje oblike koja nam nudi priroda kad je riječ o snježnim pahuljicama.

Ponavljanje nestabilnosti u nedogled rezultira u oblicima koji se i kod snježnih pahuljica nazivaju dendritima (Slika 21). Riječ dendrit kod snježnih kristala znači oblik nalik krošnji stabla (jela) ili tvorevinu nalik grančici paprati. Grananje je efekt spore difuzije molekula vode u zraku i jako ovisi o tlaku zraka. U rijetkom zraku (nizak tlak) efekti difuzije slabo utječu na rast pa je nestabilnost grananja slaba i oblik je blizak prizmi.

Što je veći tlak zraka grananje je jače izraženo. Nadalje, svaka kristalna grančica i svaki izdanak prolazi procese koje su opisani bilo da se radi o rastu kontroliranom strukturom površine bilo da se radi o difuzijom kontroliranom rastu. Najčešće radi se o miješanim utjecajima. Na primjer, gledajući mikroskopski, čim je dio površine (izdanak i slično) ispremrežen stepenicama on je podložan postupku facetiranja.

Facetirni djelić površine ima nužno oblik heksagonske prizme, a to znači da je podložan Mullins-Sekerka nestabilnosti. Posljedica je novi izdanak i opis se ponavlja u svih 5 preostalih heksagonskih smjerova (jedan je rezerviran za nošenje izdanaka). Lijep primjer prikaza posljedica opisanih procesa vidljiv je na Slici 22 koja objedinjuje nekoliko složenih oblika naraslih uglavnom u uvjetima kontrole rasta difuzijom u različitim dijelovima SAD-a. Slika 22 predstavlja uvećanu prigodnu marku izdanu uoči zime 2006.

Treba na kraju podvući da su facetiranje i grananje dva suprostavljena procesa koja se natječu pri rastu snježnih pahuljica. Ta međuigra vrlo je delikatna i jako ovisi o temperaturi i vlazi , veličinama koje se mogu brzo i znatno mijenjati u oblacima tijekom rasta pahuljica, kao i tlaku zraka. Velika raznolikost oblika sada postaje bliža i jasnija.

Puni smisao dobiva i često javno nagađanje o nemogućnosti da se pronađu dvije jednake pahuljice. Ovo razglabanje odnosi se na 'vidljivi spektar' oblika, na pahuljice koje su toliko velike da su nužno kompleksnog oblika. Ekstremno je mala vjerojatnost da se nađu dva jednaka primjerka. I uostalom što je to jednako? Na kojoj razini? To i nije samo filozofsko pitanje već traži strožu definiciju. Jednostavni oblici tipa prizmi, obično mali, često mogu dati jednake pahuljice.

Na kraju priča o snježnoj pahuljici je prilično jednostavna i može se uokviriti u dijagram prikazan na Slici 23 i čak pomalo zapanjujuća. Bez dubokog promišljanja može se reći da cijela kompleksna, prekrasna, simetrična struktura -skulptura doslovno nastaje iz zraka kotrljajući se kroz oblake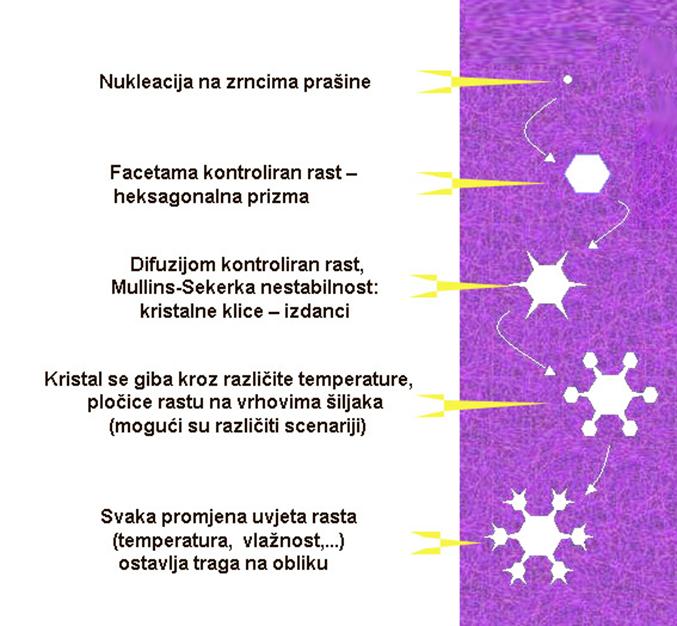

Simetrija pokazuje da svaki izdanak ima jednako okruženje i prošlost. U uvjetima turbulentnih i dinamičnih oblaka malo je vjerojatno da će se dogoditi jednaki uvjeti za različite pahuljice, pa je i malo vjerojatno očkivati dva jednaka kristala.

Na kraju treba priznati da ostaje puno otvorenih pitanja na koja za sad nema pravih odgovora. Uglavnom uspjeli smo prepoznati i opisati pojavne oblike i pojave te na kvalitativnoj razini ukazati na moguće fizikalne uzroke. Još puno treba naučiti da bi se ozbiljno uzdrmao tako kompleksan problem kao što je oblik i rast snježnih pahuljica. No dvije stvari su neosporne. Istraživanje snježnih kristala je fascinantan slučaj temeljnog studija per se unutar fizike kristala koje zahtijeva duboko razumijevanje i dinamike solidifikacije i formacije morfoloških uzoraka na razini nanoskale. Istraživanjem snježnih kristala stječe se bolji uvid u brojne fundamentalne aspekte znanosti o metrijalima

Zahvaljujem kolegama, prije svih, dr. I. Avianiu, pa zatim dr. J. Gladiću i dr. D. Lovriću na korisnim sugestijama koji su tekst učinili razumljivijim i čitljivijim. Također zahvaljujem prof. K. Libbrechtu na predivnim fotografijama snježnih pahuljica koje su me očarale i, kao i mnogima prije mene, zarobile mi dušu.