Hidrostatički tlak posljedica je težine fluida. Ako fluid ima gustoću ρ, a visina stupca fluida je h tada je hidrostatički tlak p na dnu stupca jednak

p=ρgh

gdje je g ubrzanje Zemljine sile teže.

Brzinu promjene ili, posebno, brzinu porasta veličine G definiramo kao promjenu DG po vremenu Dt

DG/Dt

Na primjer, brzina promjene puta je brzina gibanja.

Jednadžba stanja idealnoga plina povezuje tlak p, obujam V i termodinamičku temperaturu T u uvjetima termodinamičke ravnoteže idealnoga plina. Jednadžba glasi

pV=k_BNT

Ovdje je k_B Boltzmannova konstanta koja iznosi k_B=1,38·10^-23 JK^-1, a N broj molekula idealnoga plina u obujmu V.

Promjenu obujma kugle DV za male promjene polumjera Dr možemo izračunati ovako: obujam kugle polumjera r je V(r)=4πr³/3, a one s polumjerom r+Dr je V(r+Dr)=4π(r+Dr)³/3. 

Promjena obujma kugle je DV=V(r+Dr)-V(r)=4πr²Dr+o(Dr), gdje je o(Dr) funkcija promjene polumjera koja sadrži članove s drugom i trećom potencijom od Dr. 

Za male promjene polumjera Dr, funkciju o(Dr) smijemo zanemariti u odnosu na 4πr²Dr. Na primjer, za r=1 i Dr=0,1 je o(Dr)=0,13, a 4πr²Dr=1,257. Stoga, nećemo mnogo pogriješiti ako uzmemo da je DV=4πr²Dr.

Sila otpora u tekućini (fluidu) posljedica je viskoznosti ili unutarnjeg trenja promatranog fluida. Ako su brzine gibanja kugle polumjera r kroz fluid male, dobro vrijedi Stokesov zakon otpora koji pretpostavlja linearnu zavisnost o brzini v, a glasi

F=6π η rv

Koeficijent η naziva se koeficijentom dinamičke viskoznost fluida. Na drugoj strani, za velike brzine gibanja kugle kroz fluid vrijedi kvadratni zakon otpora

F=½cρr²v²π

gdje je c otporni broj ili aerodinamički faktor. Otporni broj je funkcija Reynoldsova broja, a ovisi i o obliku tijela koje se giba kroz fluid. Funkcija c=c(Re) dobivena je mjerenjima, a njezin graf nalazi se u udžbenicima iz mehanike fluida. Koji zakon uzeti u našim razmatranjima? Mi smo uzeli kvadratni zakon otpora i dobili dobro slaganje s eksperimentalnim vrijednostima. Za Re=10 iz eksperimentalnog grafa funkcije c=c(Re) možemo očitati da vrijednost c iznosi približno 3.

Drugi Newtonov zakon osnovni je zakon mehanike i polazna točka za proučavanje gibanja sustava ’’velikih’’ dimenzija (gibanje automobila, planeta, fluida, ali ne i gibanje elektrona u atomima i molekulama.), a glasi

F=ma

Ako ukupna sila F djeluje na sustav mase m, sustav će dobiti ubrzanje a. 

Drugi Newtonov zakon primijenjen na promatrani mehanički sustav naziva se i jednadžbom gibanja toga sustava.

Viskoznost ili unutrašnje trenje je posljedica prijenosa količine gibanja između slojeva fluida u gibanju. Molekule fluida zbog toplinskog gibanja prelaze iz sloja u sloj i time prenesu količinu gibanja koju su imale zbog gibanja sloja iz kojeg dolaze.

Reynoldsov broj definira se relacijom

Re=ρvl/η

gdje je ρ gustoća fluida, v brzina strujanja, η koeficijent dinamičke viskoznost, a l karakteristična duljina za promatrano tijelo. Na primjer, za kuglu, l je promjer kugle. 

Reynoldsov broj pokazuje koliki je omjer člana ma i sile otpora (sila uslijed viskoznosti) u jednadžbi gibanja. Ako je Re manji od kritične vrijednosti, tada član ma smijemo zanemariti. U našem zadatku uzeli smo da je kritična vrijednost veća od 10.

Daltonov zakon govori o tlakovima pojedinih vrsta plinova u smjesi plinova, a glasi: Tlak smjese jednak je zbroju parcijalnih tlakova plinova koji čine smjesu. Parcijalni tlak određenog plina u smjesi je onaj tlak koji bi taj plin imao kada bi sam zauzimao obujam koji zauzima smjesa. Primijenjen na atmosferu, Daltonov zakon nam omogućava određivanje parcijalnih tlakova plinova prisutnih u atmosferi poznavanjem njihovih udjela u atmosferskom zraku. Tako, ako je kisik prisutan u zraku udjelom od 21%, tada će i njegov parcijalni tlak biti 21% od ukupnog tlaka zraka.

Difuzija je proces prodiranja čestica jedne tvari među čestice druge tvari, zbog nasumičnog, termičkog gibanja. Najčešće govorimo o difuziji otopljene koja se u određenoj koncentraciji nađe u jednom dijelu obujma sredstva. Da bismo opisali proces difuzije, promotrimo sljedeću situaciju: zamislimo posudu koja je na proizvoljnom mjestu pregrađena, tako da postoje dva odjeljka A i B. Neka su oba odjeljka ispunjena istom tekućinom koja sadrži neku tvar u većoj koncentraciji u odjeljku A i manjoj koncentraciji u odjeljku B.

U određenom trenutku t = 0 maknemo pregradu, tako da se sve čestice (i čestice otopljene tvari i čestice otapala) mogu slobodno gibati u cijelom obujmu posude. Kako vrijeme odmiče, tako se koncentracija c_A smanjuje, a c_B povećava, sve dok se ne izjednače. Vrijeme potrebno za izjednačavanje koncentracija nazivamo vrijeme difuzije (ovako definirano vrijeme difuzije nije mjerljivo, odnosno kvantitativno je neodredljivo, pa se obično uvode mjere kao što su vrijeme poluživota difuzije (vrijeme potrebno da se koncentracija smanji na polovicu početne vrijednosti, i sl.) t_dif. U ovom procesu izgleda kao da su se čestice tvari usmjereno izmještale iz područja A u područje B. Kako je to moguće ako je proces difuzije posljedica nasumičnog, kaotičnog gibanja?

Čestice otopljene tvari nasumično se gibaju, što znači u svim smjerovima.  Budući da makroskopski gledano tekućina miruje, zaključujemo da se ukupna količina gibanja po svim smjerovima poništava. Gledamo li samo horizontalni smjer, na nekom proizvoljnom poprečnom presjeku kroz obujam posude, čestice otopljene tvari prelaze i slijeva nadesno i zdesna nalijevo. No, budući da s lijeve strane ima više čestica otopljene tvari, broj čestica koje prolaze slijeva nadesno veći je od broja čestica koja prolaze zdesna nalijevo. Kažemo da postoji neto difuzija iz područja veće koncentracije u područje manje koncentracije otopljene tvari. Neto difuziju, dakle, opisuje razlika apsolutnog broja čestica koje se gibaju u jednom smjeru od apsolutnog broja čestica koje se gibaju u suprotnom smjeru. Kada se, nakon t_dif , koncentracija otopljene tvari izjednači u cijelom obujmu otapala, neto difuzija postaje jednaka nuli - no to ne znači da je gibanje čestica prestalo! Čestice (i otopljene tvari i otapala!) i dalje se gibaju, no više nema preferiranoga smjera za neto izmještanje.

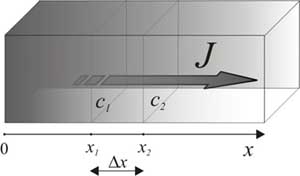
Da bismo matematički opisali proces difuzije, definirajmo smjer izmještanja difundirajuće tvari kao smjer x. Promotrimo dvije plohe, okomite na smjer izmještanja difundirajuće tvari, koje su na međusobnoj udaljenosti Δx=x₂-x₁. Neka je na poziciji x₁ koncentracija c₁, a na poziciji x₂ koncentracija c₂. Kvocijent

Δc/Δx=(c₂-c₁)/(x₂-x₁)

se naziva koncentracijski gradijent. Budući da je, u našem primjeru, za x₂>x₁ koncentracija c₂<c₁, koncentracijski gradijent ima negativan predznak. Broj čestica ΔN koje će se premjestiti u vremenu Δt od plohe 1 do plohe 2, razmjeran je koncentracijskom gradijentu. Kvocijent ΔN/Δt opisuje brzinu kojom se difundirajuće čestice izmještaju. Ta je brzina razmjerna koncentracijskom gradijentu i veličini površine plohe kroz koju se odvija difuzija,

ΔN/Δt ~ -S(Δc/Δx)

Za pisanje jednakosti uvodimo koeficijent proporcionalnosti D, kojega nazivamo koeficijent difuzije, pa gornji izraz postaje

ΔN/Δt=-D∙S(Δc/Δx)

Ovaj je izraz poznat pod nazivom Prvi Fickov zakon difuzije.