|
e-škola ¤
O projektu ¤
Fraktali ¤
Kochova krivulja ¤
Mandelbrotov skup ¤
Fraktali oko nas ¤
Literatura ¤
Helge von Koch, švedski matematičar 1870 - 1924

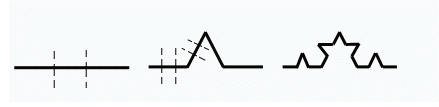
Kako nastaje Kochova krivulja?
- Uzmete ravnu crtu zadane duljine.
Podijelite dužinu na tri dijela, pa srednji dio zamijenite dvjema jednakim dužinama,
koje će jedna s drugom zatvarati kut od 600. Isti postupak ponovite još jednom,
pa još jednom, i tako dalje, u nedogled.
Zadatak 1.
Ako je duljina pocetne crte 1, koliko iznosi duljina L(n) Kochove krivulje nakon
2,3,4,5,....,n, iteracija? Prikažite u tablici i na grafikonu! Pokušajte naći
opću formulu !
Zadatak 2.
Nacrtajte fraktal prema zadanoj uputi. Dobit ćete povrće nalik na cvjetaču.
Na ovoj slici vidimo iterativni postupak koji upravlja rastom fraktala.
Kvadratu se pridodaje jednakokračni trokut, zatim na njegove katete novi kvadrati,
i tako dalje, u nedogled.
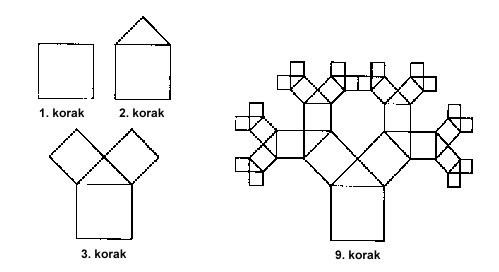
Na slici je postupak ponovljen do devetog koraka. Možete li nastaviti sami,
recimo do 20. koraka, ili još dalje? Pokušajte rukom, ili napravite kompjutorski
program i iscrtajte sliku s većim brojem iteracija.
Zadatak 3 i 4.
Evo kako nastaju još dvije vrste fraktala –
a) stablo jele
b) puževa kućica
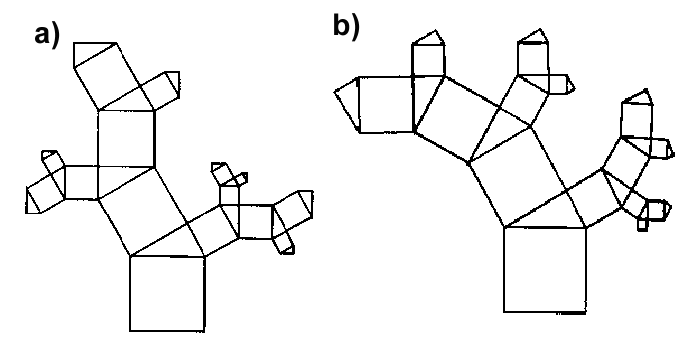
Znate li nastaviti postupak? Kako izgledaju ovi fraktali nakon 30 iteracija?
RJEŠENJE ZADATKA >>>
|

