|
e-škola ¤
O projektu ¤
Fraktali ¤
Kochova krivulja ¤
Mandelbrotov skup ¤
Fraktali oko nas ¤
Literatura ¤
SVOJSTVO SAMOSLIČNOSTI
Fraktali imaju svojstvo samosličnosti:
Svaka sljedeća od ove tri prikazane slike nastala je povećanjem malog djelića prethodne slike.
Možda ste ih već negdje vidjeli i pitali se kako nastaju.
Jesu li uvijek obojeni? Ili ima i crno-bijelih fraktala?
ITERACIJA – postupak koji se uzastopno ponavlja
Fraktalne slike nastaju iteracijom –
upornim uzastopnim ponavljanjem
nekog računskog ili geometrijskog postupka.
Fraktali su, dakle, slike nastale ponovljenim matematičkim računom ili
geometrijskom konstrukcijom.
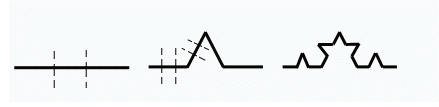
Na slici dolje možete vidjeti kako nastaje Kochova krivulja ili krivulja snježne pahuljice.
Uzmete ravnu crtu zadane duljine.
Podijelite dužinu na tri dijela, pa srednji dio zamijenite dvjema jednakim dužinama,
koje će jedna s drugom zatvarati kut od 600. Isti postupak ponovite još jednom,
pa još jednom, i tako dalje, u nedogled.
|
Za razliku od poznatih geometrijskih objekata,
oni nisu ni 1-dimenzionalne krivulje ni 2-dimenzionalni likovi, već nešto između.
Fraktal koji se može prikazati u ravnini ima dimenziju između 1 i 2.
Kako se određuje dimenzija fraktala
|
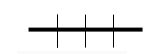
1 dimenzija: N dužina,
svaka je duljine r: Nr1=1
|
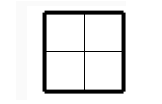
2 dimenzije: N kvadrata, svaki
je površine r2: Nr2=1
|
|
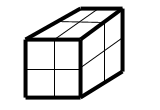
3 dimenzije: N kocaka, svaka
je volumena r3: Nr3=1
|
Fraktalna dimenzija se
općenito može definirati kao:
|
|
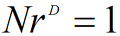
|
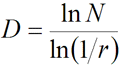
| |
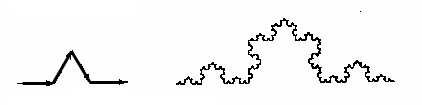
Evo nekoliko primjera kako se računa fraktalna dimenzija:
|
Jedinična dužina razdijeljena je na 3 jednake manje
dužine. Svaka je dugačka
1/3 jednične dužine: r=1/3, N=4, dimenzija ovog fraktala: D=ln(4)/ln(3)=1.26
|
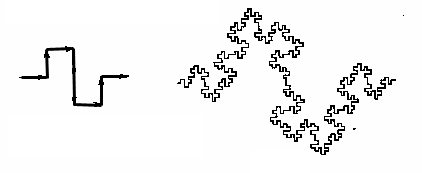
|
Jedinična dužina razdijeljena je na 4 jednake manje
dužine. Svaka je dugačka
1/4 jednične dužine: r=1/4, N=8, dimenzija ovog fraktala: D=ln(8)/ln(4)=1.5
|
|
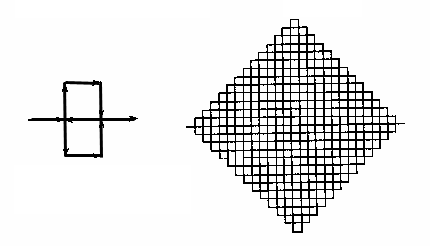
Jedinična dužina razdijeljena
je na 3 jednake dužine (r=1/3) i svaka se zamjenjuje uzorkom od 9 manjih dužina:
N=9. Dimenzija ovog fraktala: D=ln(9)/ln(3)=2
Kod ovog fraktala, za razliku od prethodna dva, kada 1/r teži u beskonačnost fraktal potpuno
prekriva ravninu, D=2.
|
|

