Ponekad mislimo da je matematika suhoparna i da joj nedostaje mašte. Benoît Mandelbrot dokazao je suprotno. Njegovo će ime ostati zapamćeno po skupu točaka koji se, naravno, naziva Mandelbrotov skup!       Benoît Mandelbrot, matematicar Roden 1924. u Poljskoj, školovan u Francuskoj, živi i radi u SAD

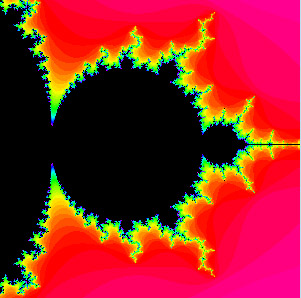
Mandelbrotov skup je najsavršeniji od svih fraktala. Kad povećamo njegove dijelove, ponovno se ukazuju isti oblici – on ima svojstvo samosličnosti Mandelbrotov skup zapravo je skup koji obuhvaća samo neke, točno zadane, točke T(a,b) u ravnini Ako te točke, dakle one koje pripadaju Mandelbrotovom skupu, prikažemo crnom bojom, a sve ostale bijelom (ili ih uopce ne nacrtamo), dobili smo crno-bijelu sliku koja predstavlja pravi Mandelbrotov skup.

Kakvim se postupkom odreduje koje točke T(a,b) pripadaju Mandelbrotovom skupu, a koje ne ?.

Iteracijom izraza:
z_n+1=z_n² + c

z i c su kompleksni brojevi:
z_n=x_n+iy_n    c=a+ib

gdje je i je imaginarna jedinica.

Prema tome, izraz za iteraciju može se napisati tako da se realni dio odvoji od imaginarnog dijela kompleksnog broja, i dobije se:

x_n+1=x_n² - y_n² + a
y_n+1=2 x_n y_n + b

Za neke vrijednosti a i b, apsolutne vrijednosti |x| i |y| postaju sve veće i veće. Možemo, primjerice, isprobati N=500 iteracija. Ako vrijednosti ni tada ne prelaze 2, tada tocka T(a,b) pripada Mandelbrotovom skupu. Prikazujemo je crnom mrljicom na mjestu (a,b) u ravnini.
ZADATAK 5

a) Izračunajte parove brojeva xn i yn za početne vrijednosti x0=0 i y0=0, za tocku a=0.1, b=0.3, do n=500. Uvjerite se da točka T(a,b) pripada Mandelbrotovom skupu. Napravite kompjutorski program koji računa tablicu, i bilježi tocke koje pripadaju Mandelbrotovom skupu.

b) Napravite program koji računa tablicu za 10x10 točaka unutar područja ravnine zadanog s 1>a>-2, i 1.5>b>-1.5.
Nacrtajte sve dobivene točke.

c) Ponovite za N=30, 100 i 1000.

UPUTA:Prvih nekoliko redaka tablice za zadanu točku T(a=0.1, b=0.3 izgledat će otprilike ovako:

x₁=0.1000 y₁=0.3000
x₂=0.0200 y₂=0.3600
x₃=-0.0292 y₃=0.3144
x₄=0.0020 y₄=0.2816
x₅=0.0207 y₅=0.3011
x₆=0.0098 y₆=0.3125

Ni u daljnjim parovima brojeva nijedan od njih ne premašuje vrijednost 2, dakle tocka (0.1,0.3) pripada Mandelbrotovom skupu.

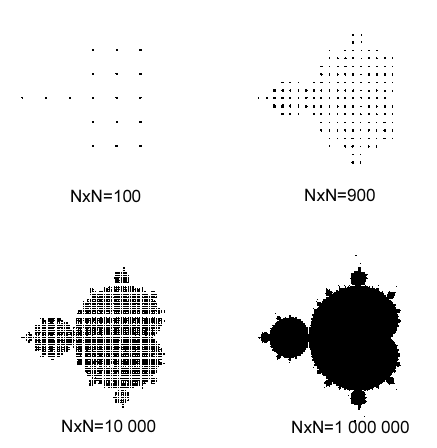
Dakle, ponavljamo postupak za različite brojeve N?N=N2 točaka podjednako razmještenih u ravnini.

Slika je preciznija, ako je mreža točaka koje ispitujemo finija, .tj. što je broj N veći..

 

Na slici lijevo vidi se kako izgledaju dobiveni skupovi za: a) N=10, N2=100 b) N=30, N2=900 c) N=100, N2=10000 d) N=1000, N2=1000000 Broj iteracija: n=500

|Fraktali | |Kochova krivulja | |Mandelbrotov skup | |Fraktali oko nas |