|
|
|
igitalni sustav je neraskidivo vezan uz razvoj računalske tehnologije. Računalima je
zbog prirode elektroničkih komponenti mnogo lakše raditi samo s dva broja ("1"-kada teče struja
i "0"-kada struja ne teče) nego s deset znamenaka koliko zahtjeva decimalni način zapisivanja
brojeva.
U tablici dolje, dan je primjer nekoliko brojeva zapisanih u decimalnom i binarnom sustavu.
|
|
| DECIMALNI | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 15 | BINARNI | 1 | 10 | 11 | 100 | 101 | 110 | 110 | 1010 | 1011 | 1100 | 1111 |
|
|
Kao što se iz ovih nekoliko primjera može vidjeti, veliki broj u binarnom sustavu
je mnogo veći nego njegov ekvivalent u decimalnom sustavu. Npr. decimalni broj 43
u binarnom sustavu je 101011. Ta prividna kompliciranost binarnog zapisa ne predstavlja
ni najmanji problem za procesore u računalima ili CD playerima jer su oni u stanju obraditi
i stotinu tisuća brojeva u jednoj jedinoj sekundi. Postoji jedna velika prednost binarnog sustava a sastoji se u tome da se brojke 0 i 1 mogu prikazati na mnogo različitih načina. Na digitalnim trakama magnetiziranost sitnog dijela trake predstavljat će broj 1 a odsustvo magnetizacije je ekvivalent za broj 0. Na sličan način binarni kod može zapisati pomoću izbočina, koje mogu simbolizirati "1" i udubina koje odgovaraju broju "0". Na slici dolje je upravo dan shematski prikaz zapisa brojeva 3, 9 i 43 u binarnom sustavu pomoću izbočina-udubina. Na vrlo sličan način je informacija zapisana na CD-u. Kao što odmah vidimo, veći brojevi su duži što znači da ako na našem disku želimo zapisivati velike brojeve trebat ćemo više prostora nego ako se ograničimo na male brojeve. Poslije ćemo se uvjeriti da je maksimalni broj koji se može zapisati u nekom binarnom sustavu vrlo važan parametar i da on određuje kako kvalitetno će audio signal biti zapisan, i poslije reproduciran. |
|
|
 |
|
|
| Prvo se moramo upoznati s vrlo važnim pojmom s kojima se vrlo često susrećemo u računalskoj tehnologiji
ali je jednako važan i u audio tehnologiji te u svim onim tehnologijama koje se zasnivaju
na digitalnom sustavu. To je "n-bitni" (8-bitni,
16-bitni i 32-bitni) zapis. Riječ "bit" je skraćenica izraza "binarni broj" a znači
"broj u binarnom zapisu". 8-bitni zapis znači da su svi brojevi prikazani u segmentima od
osam znamenaka, od kojih je opet svaka znamenka 0 ili 1. Tako će npr. br 1 biti zapisan kao
00000001, broj 5 kao 00000101 a maksimalni broj koji se u 8-bitnom sustavu može zapisati
je naravno - 11111111, odnosno 255. U 16-bitnom sustavu brojevi su zapisanu u segmentima od
16 znamenaka pa će maksimalni broj zapisan u 16-bitnom sustavu biti 1111111111111111 odnosno
65535. Kao što smo napomenuli, binarni broj na CD-u se sastoji od niza izbočina i ravnina
koje imaju neke svoje dimenzije. Evidentno je da će broj u 16-bitnom sustavu zauzeti dva puta
više prostora na CD-u nego broj u 8-bitnom zapisu. U nastavku ćemo vidjeti zašto audio tehnologija gotovo isključivo koristi 16-bitni ili viši (32-bitni) sustav a ne 8-bitni. |
|
 |
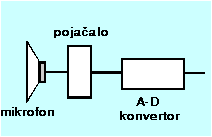Prilikom snimanja, zvuk se preko mikrofona pretvara u promjenu napona. Ukoliko zvuk želimo zapisati digitalnom tehnikom potrebno je promjenu napona ostvarenu u mikrofonu pretvoriti u niz brojeva koji će tu promjenu po mogućnosti što vjernije opisivati. Tu pretvorbu rade A-D (analog to digital) kovertori. Na sličan način, prilikom reprodukcije zvuka, signal koji je na CD-u zapisan na digitalan način treba pretvoriti u anlogni signal, što rade D-A (digital to analog) konvertori. |
|
 |
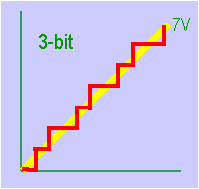Pretpostavimo da je naš A-D konvertor 3-bitni. To znači da on može zapisati samo brojke u segmentima od tri znamenke. U 3-bitnom sustavu možemo,dakle, zapisati samo brojeve od 1 (001) do 7 (111) jer broj osam (1000) zahtijeva barem 4-bitni zapis. Ako elektronički osiguramo da je prije ulaska u A-D konvertor maksimalni napon 7 V onda će naš 3-bitni konvertor pretvoriti ulazni napon u jedan od osam fiksnih napona:0,1,2,3,4,5,6 i 7 V, upravo kako je prikazano na slici lijevo. Dakle, svi naponi koji imaju vrijednost npr. između 4.51 i 5.49 V bit će u konvertoru zamjenjeni jednom jedinom vrijednošću - 5, odnosno (101). |
|
 |
Grafikon jasno pokazuje da 3-bitni procesor vrlo loše reproducira promjenu
napona. Ukoliko 3-bitni procesor promjenimo s 4-bitnim, umjesto 8 različitih napona moći ćemo sada ostvariti podjelu na 16 napona. Slika lijevo pokazuje da, kao što smo i očekivali, 4-bitna konverzija mnogo bolje prati stvarnu promjenu napona nego 3-bitna. Jasno je da što je broj bita veći da je pouzdanost s kojom se mjeri neka promjena napona bolja, odnosno, što je broj bita veći to će kvaliteta zvučnog zapisa i njegova reprodukcija biti boljh. Za tehničke potrebe čak i 8-bitna konverzija daje još uvijek pregrubu podjelu napona. Za audio potrebe uobičajeno je da se koristi 16-bitni sustav. Na taj način D-A konverter može izmjeriti 65 536 različitih napona. |
| Da sumiramo. Pomoću mikrofona zvuk se pretvara u električni signal, tj. kontinuiranu promjenu napona, koju nazivamo analogni signal.Analogni signal u A-D kovertoru se pretvara u digitalni signla i binarni kod, kao što je prikazano na slici dolje. Binarni kod se sada može zapisati na neki medij. U našem slučaju je to CD-disk gdje se binarni kod zapisuje pomoću udubina i izbočina. |
 |
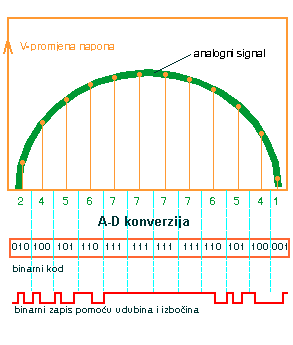Medjutim, u stvarnosti situacija je mnogo kompliciranija kada se priđe stvarnoj realizaciji zapisivanja signala odnosno njegovog dekodiranja. Pokazalo se, naime, vrlo nepraktičnim i nepouzdanim zapisivanje signala pomoću koda koji ima mnogo uzastopnih jedinica i ako se jedinice i nule često izmjenjuju, što je upravo slučaj sa standardnim binarnim kodom. Zbog toga je uvedena posebna procedura gdje se, nakon što je analogni signal pretvoren u digitalni, poduzima niz zahvata kojima se osigurava minimum vjerojatnosti pogrešnog očitavanja. Da bi se riješio gore navedeni problem česte izmjene "0" i "1" te uzastopnog pojavljivanja broja "1" uveden je takozvani "EFM - Eight to fourteen modulatiom" kod. Suština EFM koda je da poveća broj "0" u odnosu na "1" tako da je minimalni broj uzastopnih "0" dva (što se označava kao 2T) a maksimalni - deset (oznaka 10T). Tako je naprimjer broj "10" u 8-bitnom zapisu 0000 1010 a u EFM zapisu 1001 0001 0000 00. |
| No tu nije kraj komplikacijama. U binarni zapis se još dodaju tzv. paritetne provjere koje omogućavaju da se i usprkos pogrešnom očitavanju rekonstruira orginalni zapis. Primjera radi navedimo da tek oko 55% binarnog zapisa na CD-u nosi orginalnu audio informaciju a da je ostatak ugrađen u svrhu smanjivanja grešaka i rekonstruiranje orginalnog zapisa u slučaju pogrešnog čitanja. Za sve one koji žele znati više o detaljima što se sve dešava s binarnim kodom prije nego se zapiše na disk preporučam stranice Prof. Kelin.J.Kuhna sa Sveučilišta Washington. |
| Prije nego zaključimo ovo poglavlje recimo i to da za dobru i kvalitetnu reprodukciju,
nije jedino važno s koliko bita
radi A-D konvertor, nego i kolika je tzv. frekvencija sempliranja, odnosno, koliko
puta u jednoj sekund konvertor izmjeri ulazni napon. Tipična frekvencija sempliranja
u CD-ovima 44.1 kHz što znači da se analogni signal mjeri 44.100 puta u jednoj sekundi.
To može izgledati mnogo, ali treba znati da se audio signal sastoji od komponenti
različite frekvencije pa će tako najviša audio frekvencija od 20 kHZ biti izmjerena
dvaput a signal na frekvenciji od 1000 Hz bit će izmjeren 44 puta. Ako želite saznati više detalja o ovom aspektu reprodukcije zvuka svakako posjetite Philipsov "ELECTRONIC REFERENCES". |
|
 |
|
|
Za sve one koji se žele upoznati s detaljima procedure kodiranja audio signala
preporučam strnice
Prof. KELIN J. KUHN-a ELECTRONIC REFERENCES Ako želite saznati više detalja o elektronici vezanoj za reprodukciju zvuka s CD-a,Philipsov AUDIO-HANDBOOK je pravo mjesto koje treba posjetiti. Ukoliko Vas interesira video tehnologija mnogo korisnih informacija pruža Philpsov VIDEO-HANDBOOK |
 |
|
| SADRŽAJ
| MALO POVIJESTI
| DIGITALNI SVIJET
| STRUKTURA CD-a
| SVE BOJE CD-a |
|
|
ZADNJA PROMJENA: 3. ožujak 1998 |