-
©to je to teorija
perkolacije?
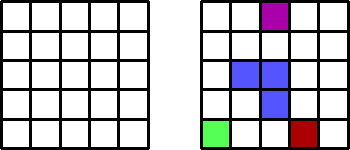
Zamislimo jednostavnu dvodimenzionalnu rešetku kao na slici gore. Neka
je svako polje popunjeno s vjerojatnošću p, neovisno o popunjenosti
susjednih polja. Popunjena polja koja su jedna drugima najbliži susjedi
(imaju jednu zajednički stranicu) nazivaju se grozdovima. Tako na desnoj
strani slike, polja koja su označena istom bojom pripadaju zajedničkom
grozdu. Kako povećavamo vjerojatnosti p, može se u sistemu pojaviti
grozd koji se prostire s jednog kraja na drugi - perkolirajući grozd. Granična
vjerojatnost na kojoj dolazi do pojave ovakvog grozda naziva se vjerojatnost
praga i označava s pc . To je vjerojatnost
na kojoj se prvi put formira perkolirajući grozd. Za 2D kvadratičnu rešetku
se dobiva pc = 0.59.
Gornja matrica i popunjena polja mogu predstavljati različite sisteme.
Njima možemo simulirati pore u nekom poroznom mediju, nečistoće u nekom
materijalu, vodljive otoke u izolatorskoj matrici ili pak nešto vrlo prozaično
kao što je princip priprave kave u automatu. Pri tome nas može zanimati
kako će neka tekućina prolaziti kroz porozni medij (npr. protok nafte kroz
različite slojeve zemljine kore) ili koliko primjesa moramo dodati nekom
materijalu da bi dobili vodič ili pak koliko kave moramo staviti u automat.
Ako stavimo premalo, neće biti dobrog okusa, a ako stavimo previše, automat
će se začepiti. Primjeri su brojni i pokušajte ih pronaći sami.
Veliki razvoj teorija perkolacije doživljava usavršavanjem kompjutera
i mogućnošću simuliranja perkolacije na velikim sustavima.
- Primjena
perkolacije u modeliranju šumskih požara
Šuma se pojednostavljeno prikazuje kao dvodimenzionalna
pravokutna rešetka. Na svakom polju se nalazi jedno drvo s vjerojatnošću
p. Takva polja nazvat ćemo "zelena polja". Neka pojedina drva
gore. Polja koja zaposjedaju stabla zahvaćena plamenom nazvat ćemo "crvena"
polja. Najjednostavniji izbor je da su na početku zahvaćena sva stabla
u prvom redu rešetke kojim modeliramo našu šumu, a da su sva ostala polja
zelena. Zanima nas da li će se požar proširiti do zadnjeg reda rešetke
(znači s jednog kraja šume na drugi) i koliko će vremena proći prije nego
što se vatra ugasi, bez obzira da li će se proširiti kroz cijelu šumu ili
će se ugasiti prije toga.
Da bismo vidjeli kako se vatra širi, moramo
prvo odrediti kriterije po kojem će se paliti stabla. U prvom slučaju ćemo
uzeti da je zeleno polje postalo crveno (stablo se zapalilo) ako postoji
susjedno crveno polje. Prilikom simuliranja krećemo od prve linije u kojoj
su sva polja crvena. Zatim prelazimo po matrici liniju po liniju i pretvaramo
zelena polja u crvena po danom kriteriju. Kad dođemo do zadnje linije ponavljamo
postupak. Svaki ovakav prijelaz po matrici predstavlja jedan vremenski
korak simulacije. Pretpostavit ćemo pojednostavljeno da u svakom ciklusu
crvena polja, nakon što su zapalila svoje susjede postaju crna polja (hrpa
pepela), koja više ne gore i ne pale okolna stabla. Simulacija je gotova
kada više nema gorućih stabala ili kada se požar proširi do zadnje linije
u matrici. Vrijeme trajanja požara je broj vremenskih koraka u simulaciji
do njenog kraja, uprosječena po više simulacija za istu vjerojatnost p.
U ovakav model se preko kriterija za širenje požara mogu uvesti i vremenske
prilike. Može se uvest kriterij da po vrućem vremenu drvo koje gori može
zapaliti ne samo najbliže, već i slijedeće najbliže susjede (to su ona
polja koja imaju zajedničke vrhove). Za slučaj vlažnog vremena uvjet da
bi se stablo zapalilo može biti da u susjedstvu mora imati dva goruća stabla.
Pojavi perkolacije u ovom modelu odgovara širenje požara kroz cijelu šumu.
Natrag na projekt

