 |
|
Tantalov vrč je hidraulična naprava za prelijevanje tekućina. Na uređaju koji ćemo izraditi može se vidjeti način njegova djelovanja. Ovo načelo se u praksi koristi u obliku gibljive cijevi, za pražnjenje posuda koje se ne mogu iskrenuti, na primjer za vađenje benzina iz spremnika automobila, ili za pretakanje iz velikih bačvi.
 Od pribora će nam trebati:
Od pribora će nam trebati:
- Prazna plastična boca od gaziranih pića, zapremnine 1 l ili 1,5 l (bezbojna) s čepom. Oštrim nožem ili škarama odrezat ćemo dno boce.
- Komad plastične prozirne savitljive cijevi promjera 10 - 12 mm, a duljine oko 60 cm.
- Sažvakana žvakaća guma.
 Na čepu treba izrezati okruglu rupu promjera koji odgovara promjeru plastične cijevi.
Na čepu treba izrezati okruglu rupu promjera koji odgovara promjeru plastične cijevi.
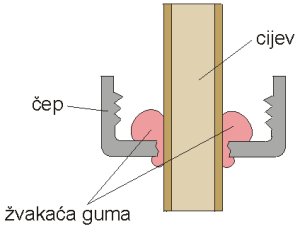 Kroz rupu na čepu provedemo cijev i okolo zabrtvimo žvakaćom gumom, jer rupa najčešće nije posve okrugla i cijev ne prianja dobro.
Kroz rupu na čepu provedemo cijev i okolo zabrtvimo žvakaćom gumom, jer rupa najčešće nije posve okrugla i cijev ne prianja dobro.
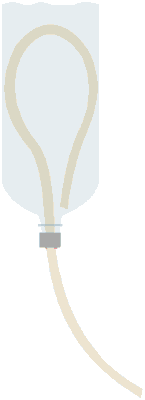 Čep zajedno sa cijevi zavrnemo na bocu, a ostatak cijevi savijemo unutra tako da kraj seže do grla boce. Time je Tantalov vrč gotov.
Čep zajedno sa cijevi zavrnemo na bocu, a ostatak cijevi savijemo unutra tako da kraj seže do grla boce. Time je Tantalov vrč gotov.
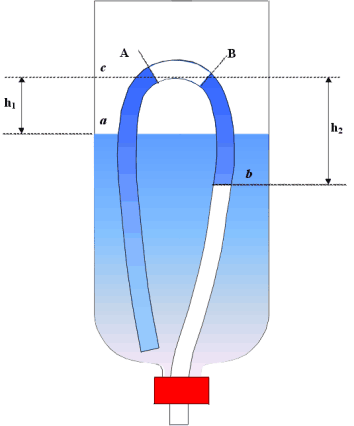
 Punimo li vrč vodom on će se ponašati kao spojene posude. Voda će imati istu razinu u vrču i u cijevi ali neće istjecati. No kad se razina vode popne do luka savijene cijevi, prelit će se i istjecati sve dok posve ne isteče, odnosno dok se stupac tekućine ne prekine ulaskom mjehurića zraka u cijev. Pri istjecanju se voda diže sa niže razine u vrču na višu razinu u preljevnoj cijevi. Kad nastane prekid, istjecanje će stati.
Punimo li vrč vodom on će se ponašati kao spojene posude. Voda će imati istu razinu u vrču i u cijevi ali neće istjecati. No kad se razina vode popne do luka savijene cijevi, prelit će se i istjecati sve dok posve ne isteče, odnosno dok se stupac tekućine ne prekine ulaskom mjehurića zraka u cijev. Pri istjecanju se voda diže sa niže razine u vrču na višu razinu u preljevnoj cijevi. Kad nastane prekid, istjecanje će stati.
OBJASNIMO POJAVU
Da bi pojasnili pojavu zamislit ćemo izdvojeni dio tekućine u gornjem luku preljevne cijevi na razini c, omeđen presjecima A i B. Vanjski tlak na otvorene površine tekućine na razinama a i b je isti i jednak je atmosferskom tlaku p0. Tlak pA na presjek A je manji od p0 za 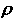 gh1, dok je tlak pB manji od p0 za gh1, dok je tlak pB manji od p0 za 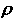 gh2. Budući da je h1 < h2, tlak pA je veći od pB za razliku gh2. Budući da je h1 < h2, tlak pA je veći od pB za razliku 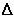 p = p = 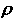 g(h2 - h1). Zato će se tekućina gibati u cijevi od A prema B, i teći sa više razine a na nižu razinu b. Brzina protoka će biti tim veća što je dulja izljevna cijev jer se time povećava visina h2. Ako u stupcu tekućine nastane prekid istjecanje će prestati. g(h2 - h1). Zato će se tekućina gibati u cijevi od A prema B, i teći sa više razine a na nižu razinu b. Brzina protoka će biti tim veća što je dulja izljevna cijev jer se time povećava visina h2. Ako u stupcu tekućine nastane prekid istjecanje će prestati.
|
 |
|
|
 |
|
|
 |
|
Autor: Hrvoje Mesić, Prirodoslovno matematički fakultet, Zagreb |
 |
 |
 |



|
|



