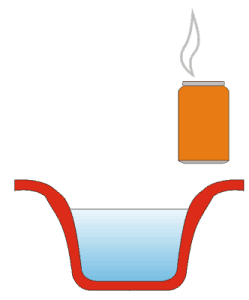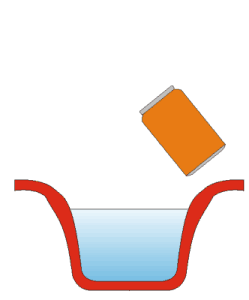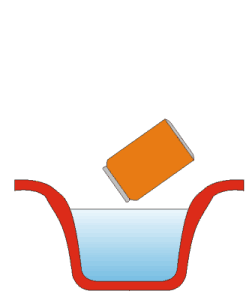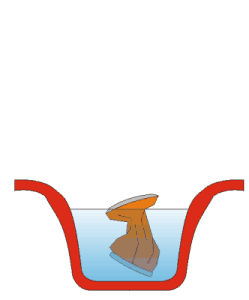U praznu limenku treba naliti vode, ali ne više nego jedan prst (oko 0,3 dl). Zatim limenku s vodom stavimo na plinsko ili električno kuhalo i pustimo da voda zavrije. Da voda u limenci vrije vidjet će se po oblaku kondenzirane vodene pare koja izlazi kroz otvor. Neka vrije 20 do 30 sekundi, tako da se unutrašnjost limenke posve ispuni vrućom vodenom parom.

U međuvremenu dok čekamo da voda zavrije treba prirediti jednu plitku zdjelicu s hladnom vodom. Dubina vode u toj zdjelici neka bude 2 - 3 cm. Koristeći krpu, da se ne opečemo, skinemo limenku sa peći i brzo ju uronimo u hladnu vodu, ali tako da joj pri tome otvor okrenemo prema dole. Istog časa kad limenka dođe u dodir s hladnom vodom neka nevidljiva sila tako će ju brzo zgužvati da će nam gotovo ispasti iz ruke.

Naglo kondenziranje vodene pare uzrokuje pad temperature u unutrašnjosti posude. Kako su tlak i temperatura u uzajamnoj vezi, smanjuje se i tlak. Smanjenje tlaka dovelo bi do usisavanja vode u limenku, ali pad tlaka dešava se puno brže nego što voda, zbog svoje viskoznosti, uspijeva ući kroz relativno uski otvor. Zato nastaje razlika u tlaku zraka iznutra i izvana, koja je dovoljna da zgnječi limenku.

Procijenimo kolika je sila djelovala.
Pretpostavimo da je temperatura pare u limenci T₁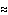370^oK, i da je unutra atmosferski tlak p₁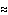10⁵Pa. Naglim hlađenjem neka se temperatura spusti na T₂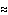300^oK. To znači da će se uz nepromijenjeni volumen novi tlak p₂ dobiti iz stalnosti omjera tlaka i temperature:

Uvrstimo li pretpostavljene vrijednosti dobit ćemo približni iznos tlaka nakon hlađenja:

odnosno razlika u tlaku iznosi p19000 Pa

Iz promjera i visine limenke koja ima oblik valjka lako se izračuna njena površina koja iznosi oko 3 dm2.
Budući da je sila umnožak tlaka i površine dolazimo do iznosa od:

Sili od 570 N odgovara težina tijela mase oko 60 kg!