|
 Da živimo u polju sile teže trebali
bi se sjetiti svaki put kad nam se desi da posrnemo ili eventualno padnemo. Da živimo u polju sile teže trebali
bi se sjetiti svaki put kad nam se desi da posrnemo ili eventualno padnemo.
Ali toliko smo se prilagodili da naše tijelo instinktivno održava ravnotežu.
Kako? Tako što mišići neprekidno postavljaju oslonac, tj. naša stopala
okomito ispod težišta tijela.
I sve dok okomica spuštena iz težišta prolazi kroz
plohu oslonca tijelo je stabilno, neće se prevrnuti.
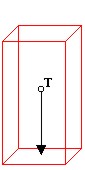  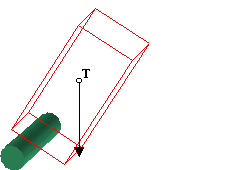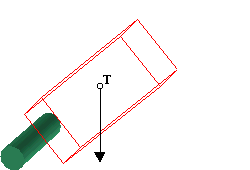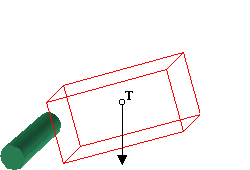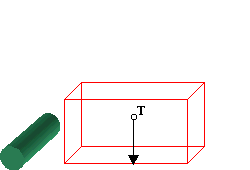
A) okomica prolazi kroz plohu oslonca: stabilno.
B) okomica iz težišta prolazi izvan plohe oslonca:
tijelo će se prevrnuti i pasti.
 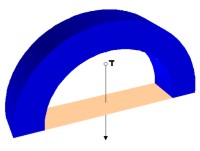 
Čak i ako se tijelo oslanja u samo nekoliko razmaknutih točaka, ono
će biti stabilno ako okomica iz težišta prolazi
plohom koju razapinju te točke.
Sve što smo do sada rekli o težištu i stabilnosti
tijela uvod je u zanimljiv pokus. Treba složiti stupac jednolikih ploča
(npr. cigle, kutije šibica, kovanice ili keksi), ali tako da ne bude uspravan
nego naprotiv što je moguće više iskrivljen, a da se ne sruši.
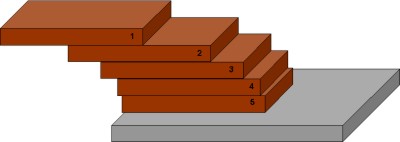
Kako to možemo postići?
Radimo li s kutijama, brojeći odozgo prema dolje počinjemo s prvom
kutijom tako da viri što je moguće više a da se ne sruši. Očito je da ćemo
ju moći izvući nešto manje od polovice njene dužine. Zatim izvlačimo drugu
i prvu kutiju zajedno sve dok ne osjetimo da bi mogle pasti i tako nastavljamo
dalje držeći se pravila da okomica od pojedinačnog težišta
gornjih kutija ne prolazi izvan plohe one kutije na kojoj leže.
Pojasnimo to grafički:
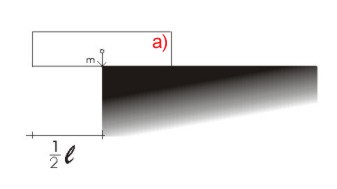
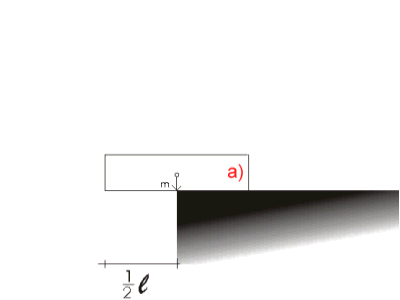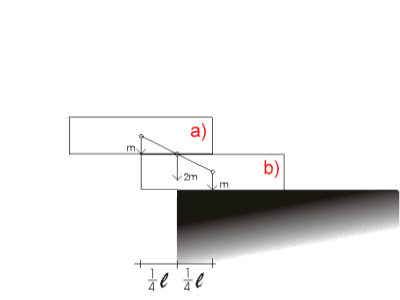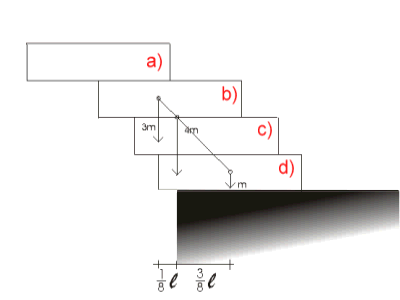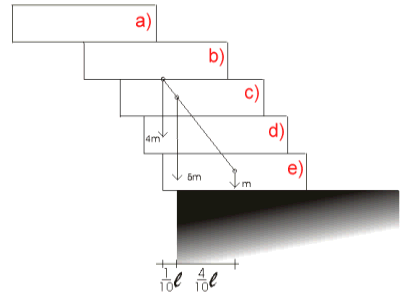
 a) Težište
prve kutije nalazi se na polovici duljine kutije i ona može biti izvučena
najviše za polovicu svoje dužine preko ruba oslonca. a) Težište
prve kutije nalazi se na polovici duljine kutije i ona može biti izvučena
najviše za polovicu svoje dužine preko ruba oslonca.
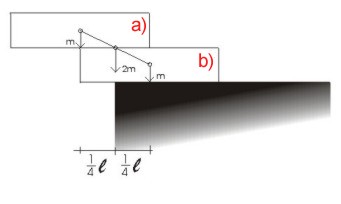
 b) Uzmimo sada prvu i drugu kutiju
(A i B) kao jedno tijelo, zajedničko težište nalazi
se na spojnici težišta pojedinih kutija. Okomica iz zajedničkog težišta
prolazi točkom koja je od ruba oslonca udaljena za 1/4 duljine kutije (l). b) Uzmimo sada prvu i drugu kutiju
(A i B) kao jedno tijelo, zajedničko težište nalazi
se na spojnici težišta pojedinih kutija. Okomica iz zajedničkog težišta
prolazi točkom koja je od ruba oslonca udaljena za 1/4 duljine kutije (l).
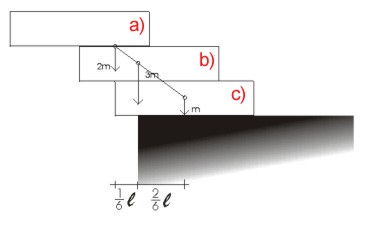
 c) Uzmemo li tri kutije, zajedničko
težište opet će biti na spojnici težišta
gornje dvije i težišta treće kutije ali će dijeliti
spojnicu u omjeru koji je obrnuto proporcionalan omjeru masa. c) Uzmemo li tri kutije, zajedničko
težište opet će biti na spojnici težišta
gornje dvije i težišta treće kutije ali će dijeliti
spojnicu u omjeru koji je obrnuto proporcionalan omjeru masa.
Dakle okomica će prolaziti točkom koja je od ruba oslonca udaljena
za 1/6 duljine kutije.
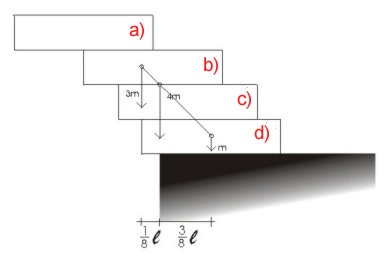
 Pogledajmo sada za koliko može
prva kutija najviše viriti preko ruba oslonca? Pogledajmo sada za koliko može
prva kutija najviše viriti preko ruba oslonca?
Zbrojimo duljine izvučenih dijelova kutija.
Za n kutija dobijemo sumu S.
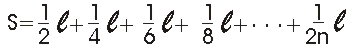
 Može se pokazati da suma ovog reda
divergira, tj. da ako uzmemo dovoljan broj članova možemo postići da nam
prva kutija proizvoljno daleko viri preko ruba oslonca. Može se pokazati da suma ovog reda
divergira, tj. da ako uzmemo dovoljan broj članova možemo postići da nam
prva kutija proizvoljno daleko viri preko ruba oslonca.
 |
|
|
 |
|
|
 |
|
Autor: Hrvoje Mesić, Prirodoslovno matematički fakultet, Zagreb |
 |
 |
 |



|
| 


